Correction épreuve de mathématiques au baccalauréat A et ABI 2020

Correction épreuve de mathématiques au baccalauréat A et ABI 2020

Exercice I / 4 pts
1.a) Résolvons dans R l’équation x2−xx2−x −2=0−2=0
Δ=9≻0Δ=9≻0 donc cette équation admet deux solutions : x1=−1×1=−1 et x2=−2×2=−2 0,75 pt
b) Développons (x−1)(x−1) (x2−x−2)(x2−x−2) = =x3−2×2=x3−2×2 −x+2−x+2 0,5 pt
c) Déduisons l’ensemble solution dans R de l’inéquation : x3−2x2x3−2×2 −x+2≤0−x+2≤0
(x−1)(x−1) (x−2)(x−2) (x+1)(x+1) ≤0≤0
Dressons le tableau de signe de x3−2x2x3−2×2 −x+2≤0−x+2≤0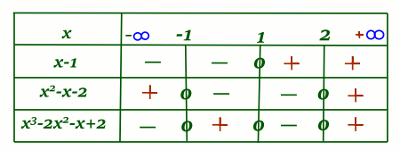
Donc l’ensemble solution est : ]−∞;−1]∪]−∞;−1]∪ [1;2][1;2] 1pt
2.a) Résolvons dans R2R2 le système (S) {2x−y=2−x+4y=6{2x−y=2−x+4y=6
En utilisant la substitution, nous obtenons : S={2;2}S={2;2} 0,75 pt
b) Déduisons -en l’ensemble solution du système {2ex−ey=2−ex+4ey=6{2ex−ey=2−ex+4ey=6
En posant X=exX=ex et Y=eyY=ey, nous retrouvons le système précèdent, SOIT {2X−Y=2−X+4Y=6{2X−Y=2−X+4Y=6
Dont {ex=2ey=2{ex=2ey=2 ⇒⇒ {x=ln2y=ln2{x=ln2y=ln2 1 pt

Exercice II / 6 pts
1. Recopions et complétons le tableau 1 pt

Classe en mois	[0;3[	[3;6[	[6;9[	[9;12[	[15;15[
Taux d’absentéisme	16%	37,5%	27,5%	15%	4%
Effectifs ( Employés )	128	300	220	120	32
Effectifs cumulés croissants	128	428	648	768	800
Effectifs cumulés décroissants	800	672	372	152	32

2. Traçons l’histogramme des effectifs 2 pts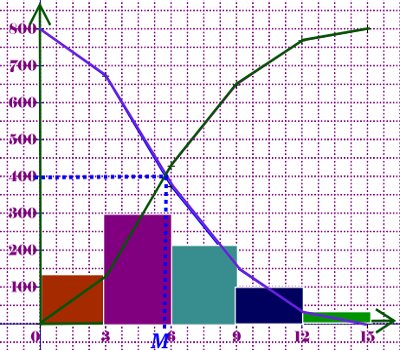

3. Traçons le polygone des effectifs cumulées croissants 1 pt
(Voir graphique 2)
4. Traçons le polygone des effectifs cumulées décroissants 1 pt
(Voir graphique 2)
5. Déterminons graphiquement la médiane 1 pt
(Voir graphique 2)

Problème 10 points
1) Déterminons par lecture graphique : 0,75 pt
f(0) = 3 ; f(1) = 2 ; f(-2) = -7.
2) Conjecturons les limites 1 pt
• limx→−∞f(x)=−∞limx→−∞f(x)=−∞;
• limx→+∞f(x)=+∞limx→+∞f(x)=+∞;
• limx→−1−f(x)=−∞limx→−1−f(x)=−∞;
• limx→−1+f(x)=+∞.
3. Ecrivons une équation de l’asymptote verticale 0,5 pt
x=−1
4. Dressons le tableau de variation de f 1 pt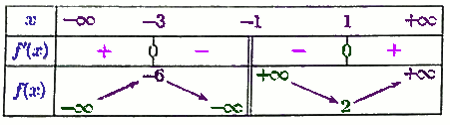
5. Reproduisons la courbe Cf et construisons dans le même repère orthonormé R=(O;→i;→j) la représentation graphique de la fonction x=|f(x)|. Unité sur les axes 1 cm 1,5 pt
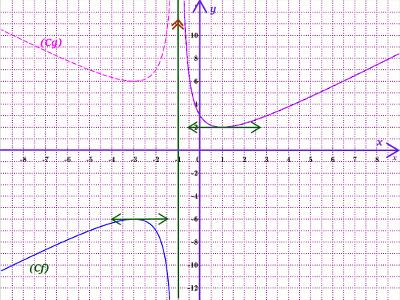1. Exprimons f(1), ; f(-2) et f(0) en fonction de a, b et c 1,5 pt
{f(x)=a+b+c2f(−2)=−2a+b−cf(0)=b+c
2. Déduisons que le triplet (a, b, c) est une solution du système 0,75 pt
{a+b+c2=2−2a+b−c=−7b+c=3
3. Recopions la solution du système. 1 pt
iii)(1,−1,4)
4. Déduisons que f(x)= x2+3x+1 1 pt
f(x)= ax+b+ cx+1 =x−1+ 4x+1 =x2+3x+1
5. Montrons que F est une primitive de f 1 pt
Il suffit de montrer que F′(x)=f(x) et F(0)=0